1877 г. Людвиг Больцман публикует работу «Основы молекул статистики» и дает обоснование понятия энтропии. В основе лежат микро- и макросостояния.
Под микросостоянием системы понимают данный способ распределения всех молекул по всем имеющимся уровням энергии с учетом различимости молекул.
Под макросостоянием системы понимают данный способ распределения всех молекул по всем имеющимся уровням энергии без учета различимости молекул.
Видео:Обратимые и необратимые процессы. Энтропия. Второй закон термодинамики. 10 класс.Скачать

Модельная система: 2 уровня энергии (E1 и E2), на каждом уровне может находиться только 2 частицы.
Для того чтобы ввести микросостояния нужно различить частицы.
Видео:Статистический смысл энтропии. Флуктуации.Скачать

Термодинамическая вероятность W — число микросостояний удовлетворяющих данному микросостоянию.
где N — число частиц в системе, n — число уровней энергии.
Видео:Что такое Энтропия?Скачать

Равнораспределение — такое распределение энергии, когда на каждом уровне находится одинаковое число частиц. Равное распределение имеет наибольшую термодинамическую вероятность.
Статистическая гипотеза Больцмана
Термодинамическая вероятность в изолированной системе всегда увеличивается при протекании самопроизвольного процесса. При этом она достигает своего максимума в состоянии равновесия.
Изолированная система всегда эволюционирует в сторону возрастания своей термодинамической вероятности.
Видео:Энтропия и вероятность. Часть 1. Макро- и микросостояния.Скачать

Разобьем искомую систему на 2 части. Как определить S, если известны энтропии частиц S1 и S2.
S — экстенсивная функция;
Видео:Что такое второй закон термодинамики?Скачать

1) дифференцируем по W1, когда W2 = const
2) Дифференцируем по W2, когда W1 = const
🌟 Видео
Информационная энтропия (видео 14) | Теория информации | ПрограммированиеСкачать

Что же такое энтропия? [Veritasium]Скачать
![Что же такое энтропия? [Veritasium]](https://i.ytimg.com/vi/g1Sdngywob4/0.jpg)
Энтропия и второй закон термодинамики (видео 6) | Энергия| БиологияСкачать

Второе начало термодинамики. Часть 5. Понятие энтропии.Скачать

Представление об энтропииСкачать
Энтропия. 10 класс.Скачать

Основы теплотехники. Второй закон термодинамики. Энтропия. Теорема Нернста.Скачать

Время и энтропия. Серия #5: В чём смысл жизни? [MinutePhysics]Скачать
![Время и энтропия. Серия #5: В чём смысл жизни? [MinutePhysics]](https://i.ytimg.com/vi/_gWkZaYd5mc/0.jpg)
ЭНТРОПИЯ | Все исправитьСкачать

Время и энтропия. Серия #1: Почему время идёт только вперёд? [MinutePhysics]Скачать
![Время и энтропия. Серия #1: Почему время идёт только вперёд? [MinutePhysics]](https://i.ytimg.com/vi/aiD51zzeuzw/0.jpg)
1 Лекция 16 Энтропия и вероятностьСкачать
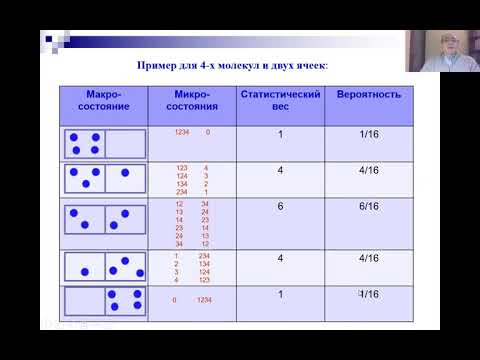
Энтропия. Равновероятные исходыСкачать

Статистическая сумма || Лекция №2 || Статистическая термодинамикаСкачать

32. Энтропия идеального газаСкачать

Энтропия и стрела времени (ScienceClic)Скачать



