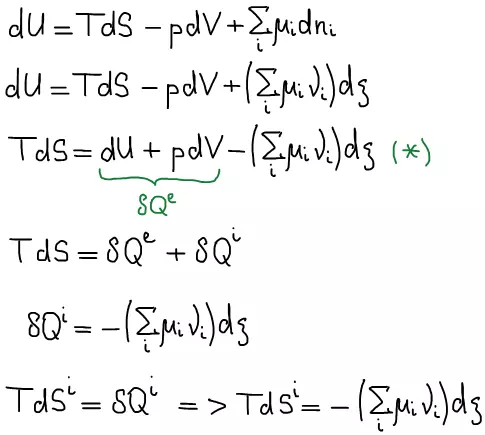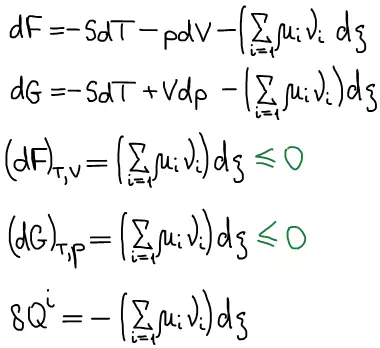Характеристические функции

Характеристическая функция — такая термодинамическая функция, по изменению которой в определенных условиях можно судить о направленности самопроизвольного процесса и о достижении состояния равновесия, а производные различного порядка которых дают нам явно и наиболее просто другие термодинамические функции и параметры системы.

Изоэнтропийно-изохорические условия:

Рассмотрим только обратимые процессы.

1. Докажем, что внутренняя энергия является характеристической функцией.

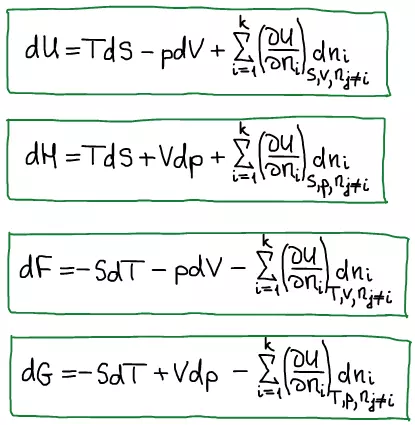
Термодинамический вид уравнения полного дифференциала внутренней энергии:

Термодинамическая система находится в состоянии истинного термодинамического равновесия при всех изменениях, совместимых с данными закрепленными значениями S и V, когда внутренняя энергия не уменьшается (либо остается постоянной, либо возрастает).

Первое уравнение Максвелла:

Таким образом, из приведенных выше рассуждений следует, что внутренняя энергия является характеристической функцией.

2. Докажем, что энтальпия является характеристической функцией.

Термодинамический вид полного дифференциала энтальпии:

Термодинамическая система находитя в состоянии истинного термодинамического равновесия при всех изменениях совместимых с данными закрепленными значениями S и p, когда энтальпия системы не уменьшается (либо H=const, либо энтальпия возрастает). Возрастание возможно в результате флуктуаций, где флуктуация — это такое изменение, которое не является термодинамическим процессом.

Второе уравнение Максвелла:

Энтальпия является характеристической функцией.

3. Докажем, что функция Гельмгольца является характеристической.

То что функция Гельгольца удовлетворяет первой части определения характеристической функции мы уже показали в 1 параграфе. Рассмотри только обратимые процессы.

Термодинамический вид уравнения полного дифференциала для функции Гельмгольца:

Третье уравнение Максвелла:

Термодинамическая система, находится в состоянии истинного термодинамического равновесия при всех изменениях, совместимых с данными закрепленными значениями T и V, когда функция Гельмгольца не уменьшается (либо остается постоянной, либо возрастает).

4. Докажем, что функция Гиббса является характеристической

То, что функция Гиббса удовлетворяет первой части определения характеристической функции мы показали в 1 параграфе.

Термодинамический вид уравнения полного дифференциала для функции Гиббса:

Четвертое уравнение Максвелла:

Термодинамическая система, находится в состоянии истинного термодинамического равновесия при всех изменениях, совместимых с данными закрепленными значениями T и p, когда функция Гиббса не уменьшается (либо остается постоянной, либо возрастает).

Видео:15. ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ 📚 Теория вероятностейСкачать

Cлучай открытой системы​

Не рассматриваем протекание химических реакций, т.е. состав может изменяться только механически: за счет обмена с окружающей средой.

Фундаментальные уравнения термодинамики:

μi — химический потенциал i-го компонента — это изменение характеристической функции при внесении в систему бесконечно большого размера 1 моль i-го компонента в условиях закрепления её естественных переменных и постоянства состава.

Химический потенциал i-го компонента — работа по обратимому внесению 1 моль i-го компонента в бесконечно большую систему в условиях либо изобарно-изотермических, либо изохорно-изотермических.

Если функция φ некоторая термодинамическая функция, то

μi — парциально мольное значение функции Гиббса по i-му компоненту (справедливо только для функции Гиббса).

Видео:Чем различаются характеристическая функция и функция принадлежности? Душкин объяснитСкачать

Cлучай закрытой системы, в которой изменение состава происходит за счет протекания химической реакции​

Одно из основных соотношений неравновесной термодинамики: